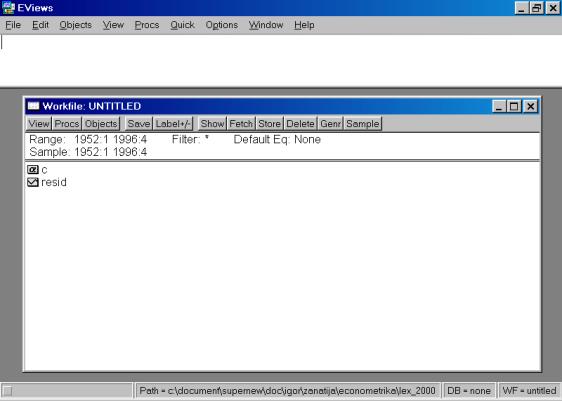
Eviews (далее пакет) установлен в директорий Program Files/Eviews3. Запуск осуществляется выбором соответствующего значка в панели Пуск/Программы/Eviews3/Eviews 3.1 (файл C:\Program Files\EViews3\EViews3.exe) (см. рис. 1) или щелчком (двойным щелчком – в зависимости от установок) по соответствующей пиктограмме на рабочем столе.

Рис. 1.

Если Вы все сделали правильно, появится стартовое окно пакета (рис.2).

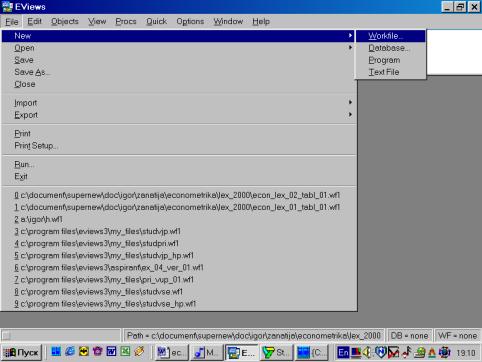
Рис. 2.

Если в настоящий момент окно, содержащее пакет, является активным, то первая строка экрана (Title Bar) будет темнее остальных. При переключении в другое окно цветовая окраска данной строки изменит цвет на более приглушенный (серый).

Ниже следует строка основного меню (Main Menu). Принцип его построения прост – при нажатии на соответствующие клавиши появляется раскрывающееся меню (drop-down menu). Доступные в настоящий момент опции являются затемненными (darkened menu items). Те пункты, с которыми в настоящий момент работа невозможна, приглушены (grayed menu items).

Далее располагается командная строка (окно) (command window). В нем происходит непосредственный набор команд, которые выполняются после нажатия клавиши Enter (Ввод). Для исполнения многих команд отсутствует необходимость их набора – просто надо выбрать нужный пункт в основном меню.

Большая часть экрана пакета отведена под рабочую область (work area). В ней размещаются рабочие объекты. Переключение между ними осуществляется нажатием клавиши F6.

Последняя область экрана показывает текущее состояние (status line) пакета (рабочий каталог, текущий файл и др.).

Завершение работы с пакетом осуществляется путем выбора в командной строке опции File/Exit. Система предложит сохранить/не сохранить имеющиеся данные. Если имя файла не было задано ранее, автоматически будет предложено имя UNTITLED. Его можно изменить на любое другое. Пакет имеет обширнуюсправочную систему (пункт основного меню Help).

Знакомство с пакетом начнем с файла, содержащего данные о совокупном спросе на деньги (M1) – (aggregate money demand) (M1) – зависимая переменная;независимые: доход (ВВП) - income (GDP); уровень цен (PR) - price level (PR); краткосрочная процентная ставка (RS) - short term interest rate (RS).

Проведем некоторые преобразования и расчеты.

Первым шагом создадим новый рабочий файл (workfile). Его имя должно иметь следующий вид и состоять только из латинских букв: Номер_группы_demo_01.wf1 (расширение wf1 присваивается автоматически). Например: 451_demo_01.wf1. Расположить его следует в директории, относящемся к Вашему факультету (внимательно ознакомьтесь с памяткой в компьютерном классе). Исходные данные находятся в файле Excel. Они должны быть импортированы в пакет. Создание рабочего файла начнем с того, что выберем File/New/Workfile в основном меню (см. рис. 3).

После нажатия на кнопке со словом Workfile откроется диалоговое окно, с помощь которого можно задать тип вводимых Вами данных (см. рис. 4).

Рис. 3.

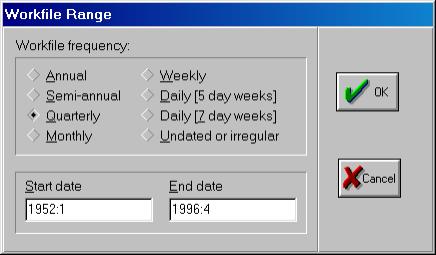
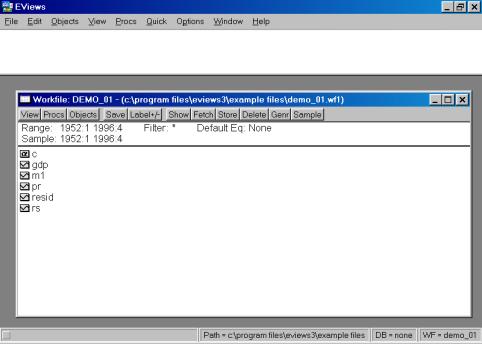
Рис. 4.

Важным является указание начальной (start) и конечной (end) даты/наблюдения (date/observation).

В нашем примере начальным периодом является первый квартал 1952 г. (1952:1), конечным – четвертый квартал 1996 г. (1996:4).

Закончив ввод временных периодов, надо нажать клавишу OK. Пакет создаст рабочий файл без имени, и на дисплее в рабочей области появится окно (см. рис. 5). Все рабочие файлы пакета всегда содержат вектор коэффициентов C и серию RESID.

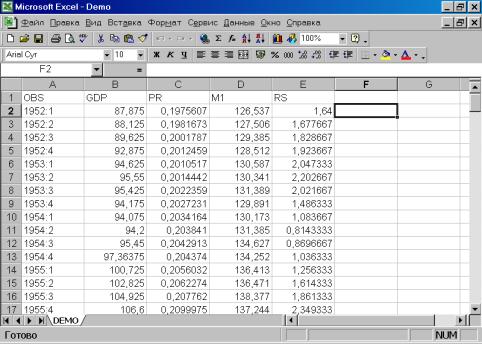
Рис. 5.

Следующим шагом является просмотр исходных данных, содержащихся в исходном файле по адресу Program Files/Eviews3/Example files/demo.xls (формат Exсelверсии 5.0 и младше). Важное замечание: имеющаяся версия пакета позволяет импортировать файлы Excel не старше версии 5.0. В противном случае будет выдано сообщение об ошибке. Всегда сохраняйте свои файлы как файлы Microsoft Excel 5.0/95. Для визуализации данных необходимо запустить табличный процессор Excel (действия аналогичны запуску Eviews). Результат представлен на рис. 6. Ознакомившись с данными, файл, подлежащий экспортированию,необходимо закрыть.

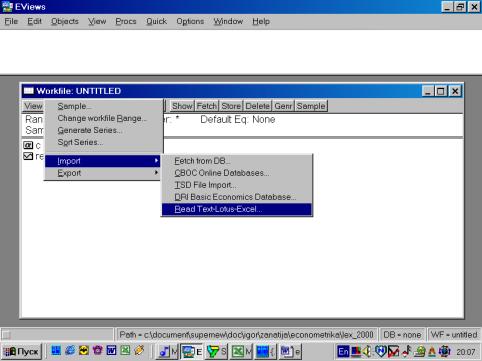
Рис. 6.

Для чтения данных, созданных в других программах, надо выбрать в рабочем файле опцию Procs/Import/Read Text-Lotus-Excel… (см. рис. 7). Появится диалог, представленный на рис. 8.

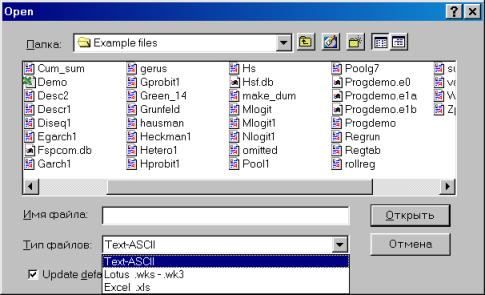
Рис. 7.

Перейдем к папке, содержащей искомый файл (для упрощения поиска в опции Тип файлов (Files of type) можно выбрать Excel.xls (см. рис.8). Для того, чтобы пакет «помнил» Ваши перемещения по папкам компьютера, можно поставить флажок в опции Update default directory (см. рис. 8).

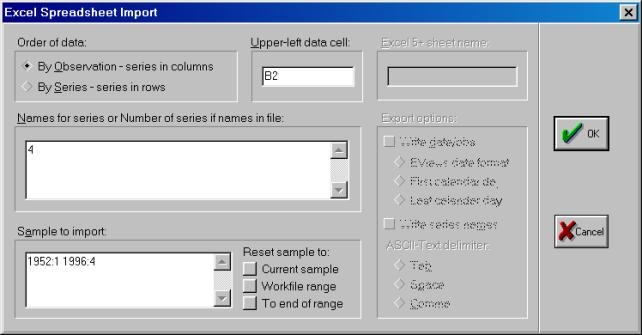
Рис. 8.

Наведем курсор на файл demo.xls и нажмем кнопку Открыть (см. рис. 8). Появится диалог открытия электронных таблиц формата Excel (см. рис. 9).

Рис. 9.

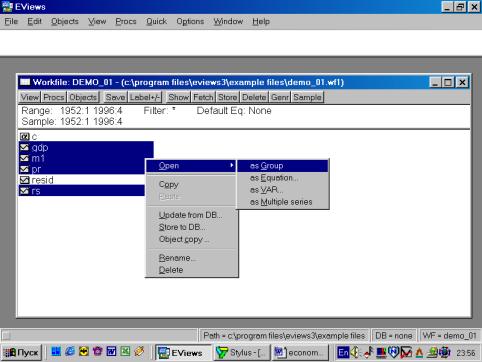
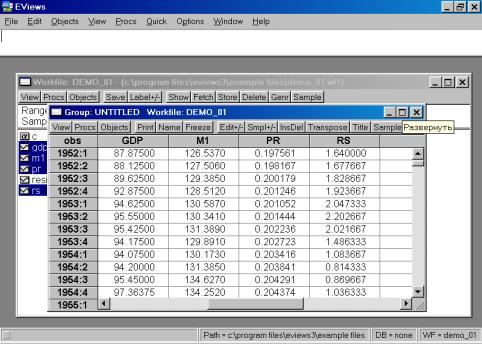
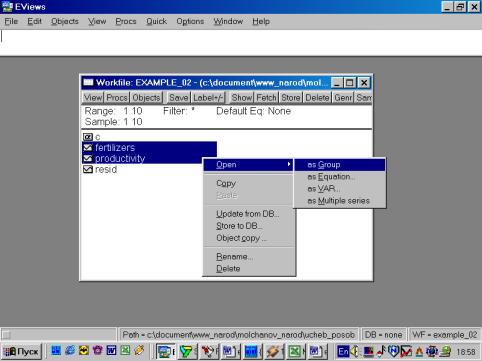
Рис. 10.

После того, как исходные данные перенесены Вами в рабочую область пакета (появились имена переменных), надо провести их верификацию (проверку правильности). Вам необходимо создать новую группу, содержащую все импортированные серии (переменные). Это делается следующим образом: необходимокликнуть мышкой по имени первой переменной (например, GNP), затем, удерживая клавишу  CTRL кликнуть по переменным M1, PR и RS. Все серии на экране будут зачернены. Затем необходимо подвести курсор мыши на зачерненную область экрана и кликнуть правой кнопкой. Далее необходимо выбрать опцию Open. Пакет откроет диалоговое окно со следующими опциями (см. рис. 11).

Выберем Open Group (открыть в одной группе). Пакет создаст группу с именем UNTITLED, в которую войдут все переменные (серии). По умолчанию, данные будут представлены в виде электронной таблицы (возможны другие варианты представления) – см. рис. 12.

Рис. 11.

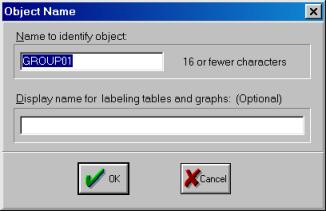
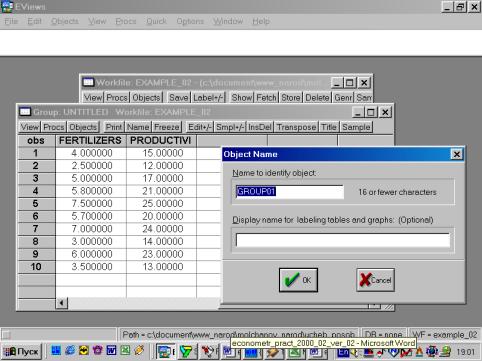
Рис. 12.

Проведите визуальную проверку корректности данных. Сравните, как разместились переменные из исходного файла, обратите внимание на столбец слева от первой переменной (он серого цвета). В нем отображены годы и порядковые номера кварталов. Полученной новой группе данных можно дать имя. Для этого необходимо нажать кнопку Name в текущем окне (см. рис. 12). Появится диалоговое окно (рис. 13.). Автоматически будет предложено имя – GROUP01. Его можно принять, нажав кнопку OK. В рабочем файле сразу добавится одна переменная с введенным Вами именем. Теперь к ней всегда можно перейти простым нажатием клавиши мыши.

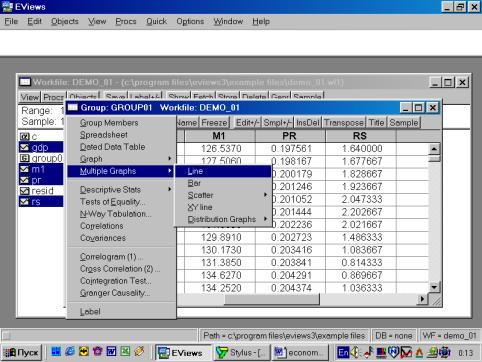
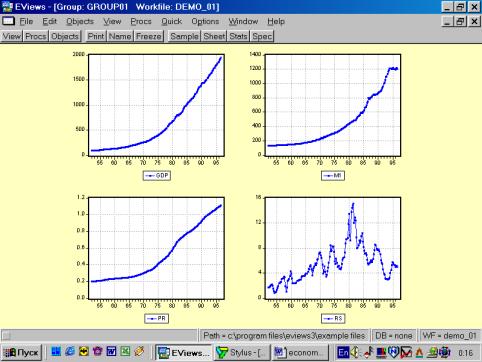
Рис. 13.

Образованную Вами группу можно просматривать не только в виде электронной таблицы. Если, находясь внутри GROUP01, выбрать последовательность командView/Multiple Graphs/Line (см. рис. 14), то данные предстанут не в виде таблицы, а как линейные графики по каждой серии (переменной) – см. рис. 15.

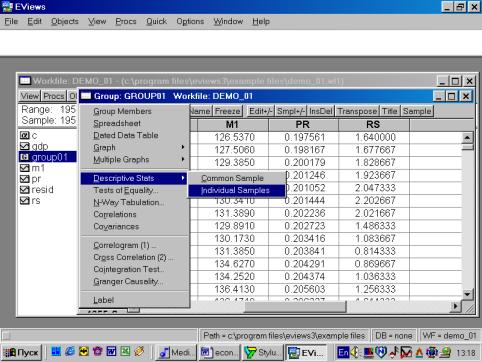
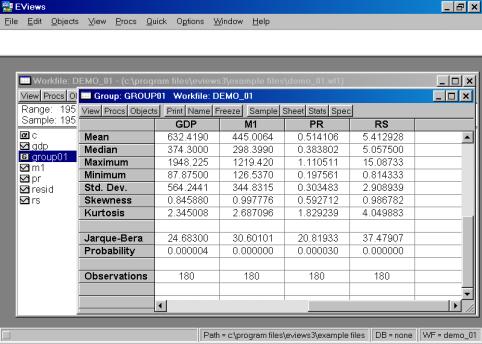
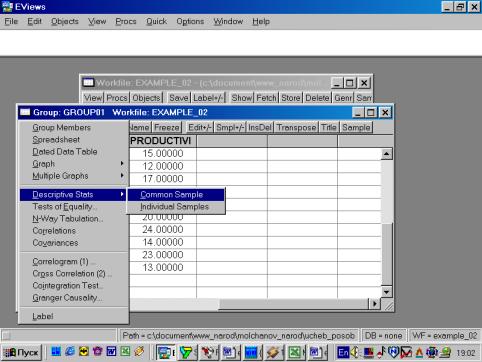
Рис. 14.

Для того, чтобы вернуться к прежней форме представления данных (например, электронной таблице), надо выбрать View/Spreadsheet.

Для просмотра числовых характеристик (описательных статистик) отмеченных переменных необходимо выбрать в рабочем файле View/Descriptive Stats/Individual Samples (см. рис. 16).

В результате появится окно, представленное на рис. 17. В нем содержатся:

Mean – Среднее арифметическое значение;

Median – Медиана;

Maximum – Максимальное значение;

Minimum – Минимальное значение;

Std. Dev. – Стандартное отклонение (среднее квадратическое отклонение);

Skewness – Коэффициент асимметрии;

Kurtosis – Эксцесс;

Probability – Вероятность;

Observations – Количество наблюдений.

Рис. 15.

Рис. 16.

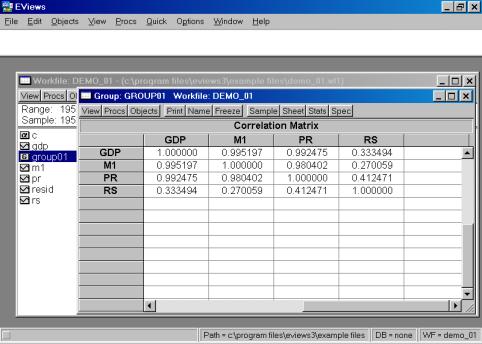
Рис. 17.

Если возникает необходимость проанализировать матрицу коэффициентов корреляции, то необходимо выбрать View/Correlations. Результат представлен на рис. 18.

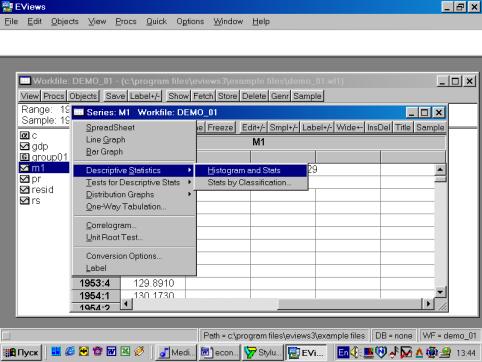
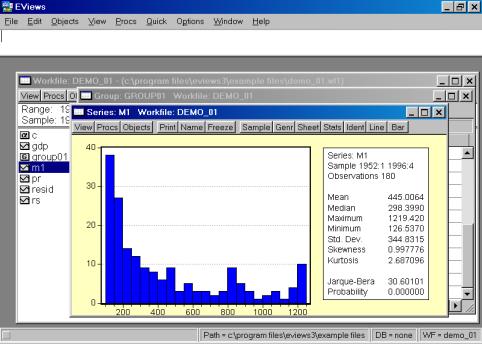
Рис. 18.

Вы также можете исследовать характеристики для отдельных серий (переменных), совместив вывод диаграммы и числовых характеристик. Дважды кликните на имени серии (например, на переменной М1)  и выберете в рабочем файле пункт меню View/Descriptive Stats/Histogram and Stats (см. рис. 19). Результат наглядно виден на рис. 20.

Рис. 19.

Рис. 20.

С другими возможностями пакета Вы познакомитесь на последующих занятиях.

Для индивидуальной работы по предложенной выше схеме предназначены нижеследующие данные. Подумайте, все ли данные необходимо заносить в электронную таблицу или импортировать из неё.

Пример 1. Стоимость однокомнатных квартир в Москве [6].

Данные из газеты «Из рук в руки» за период с декабря 1996 г. по сентябрь 1997г.

Была выбрана Юго-Западная часть города, в которой высок спрос на жилые площади (всего 69 наблюдений). Файл example_01.xls.

Найдите среднее арифметическое, выборочное стандартное отклонение и другие статистики параметров. Найдите коэффициенты корреляции параметров с ценой квартиры. Соответствуют ли полученные значения экономической интуиции?

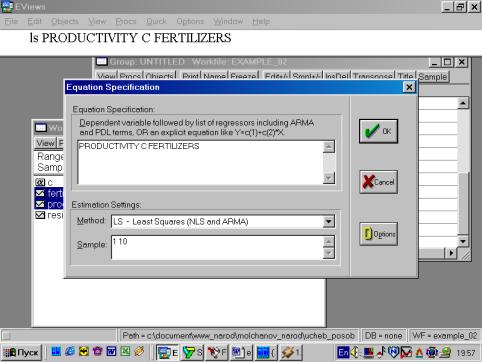
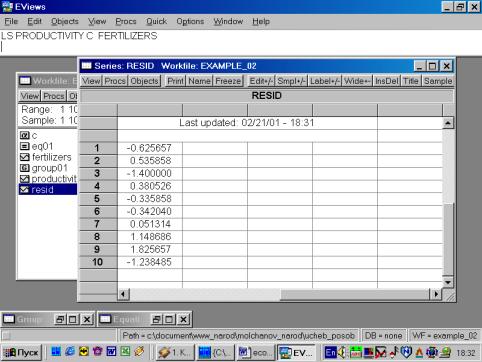
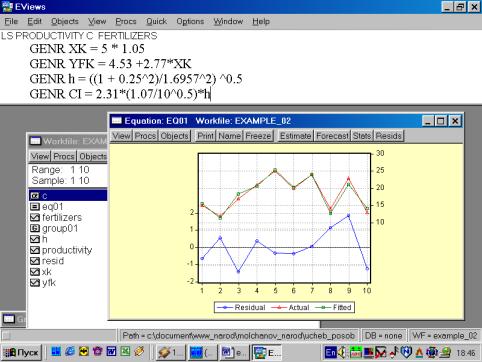
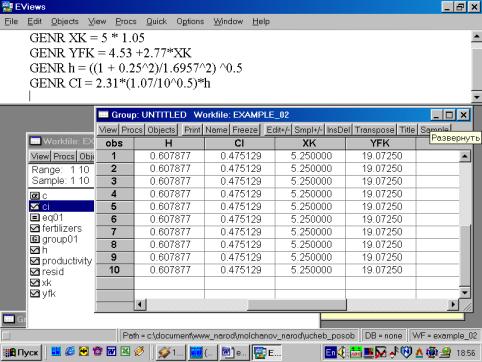
Практическое занятие № 2.

«Применение Eviews при построении и анализе линейной однофакторной модели регрессии»

Пример 2. Имеются следующие данные по 10 фермерским хозяйствам области:

Порядок выполнения задания

Рис. 27.

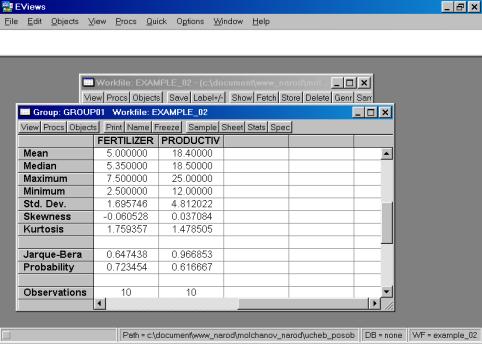
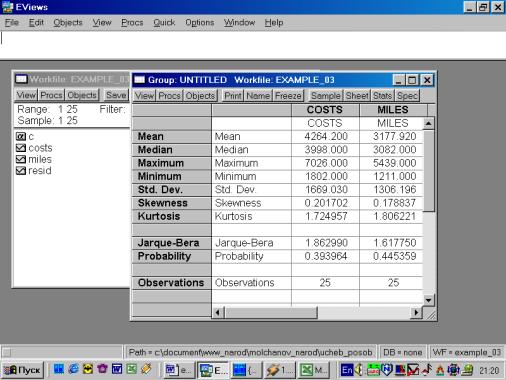
Рис. 28.

Сохраним рабочий файл (рис. 28).

4.     Значения описательных статистик находим следующим образом: в окне  workfile выделяем переменные, щелкаем мышкой по выделенной части и далее выбираем: Open/As Group/ (рис. 29). Открывается окно с исходными данными. Новую группу можно сохранить, выбрав опцию Name (рис. 30). Для просмотра описательных статистик View/Descriptive Stats/Common Sample (рис 31). Результат представлен на рис. 32.

Рис. 29.

Рис. 30.

Рис. 31.

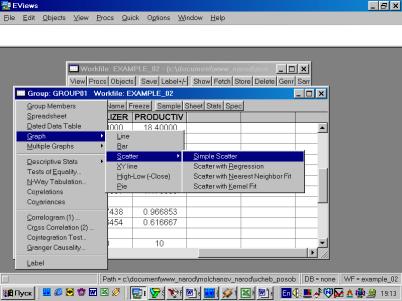
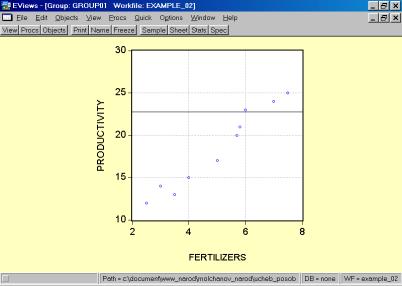
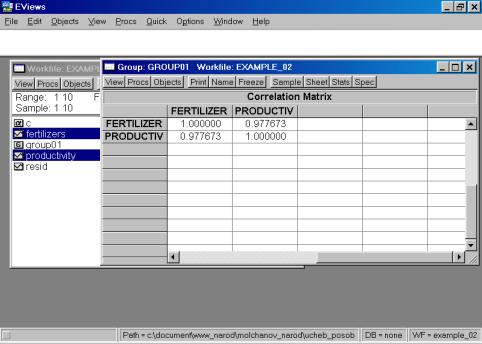
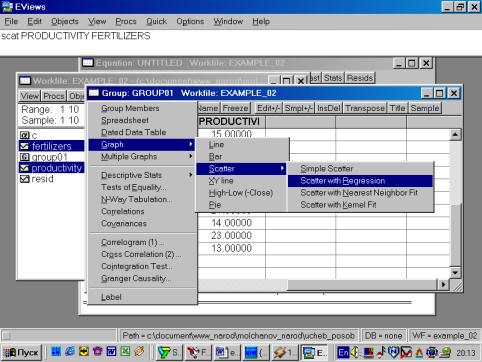
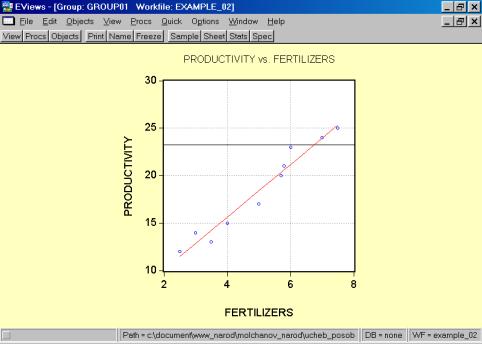
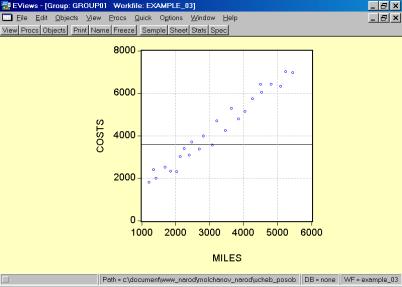
Рис. 32.

5.     В окне workfile (рис. 32) для построения поля корреляции необходимо выбрать следующие пункты меню: VIEW/GRAPH/SCATTER/SIMPLE SCATTER/(рис. 33). Полученный в результате график представляет собой поле корреляции результативного и факторного признаков (рис. 34).

6.     В окне Workfile (используя созданную группу из двух переменных) выбрать:    /VIEW/CORRELATION/ (рис. 35). Полученная таблица - корреляционная матрица, в которой отражено значение коэффициента парной корреляции результативного и факторного признаков (рис. 36).

Рис. 33.

Рис. 34.

Рис. 35.

Рис. 36.

7.     В диалоговом окне описать в общем виде искомое уравнение: LS PRODUCTIVITY C FERTILIZERS <Enter> (метод наименьших квадратов (LS) эндогенная переменная, константа, экзогенная переменная), или выбрать в строке главного меню EVIEWS: QUICK/ESTIMATE EQUATION/ PRODUCTIVITY C FERTILIZERS (рис. 37). В открывшемся окне (рис. 38) должны быть переменные: зависимая переменная, применяемый метод, число наблюдений, параметры уравнения регрессии, стандартные  ошибки, значения t – статистик и соответствующие им вероятности, значение  и ряд других показателей.

Рис. 37.

Рис. 38.

8. и 9. Результаты выполнения п.7 позволяют оценить статистическую значимость параметров уравнения регрессии и объяснить полученное значение R .

Рис. 43.

Рис. 44.

11. Данная операция возможна только в том случае, если ей предшествует построение регрессионного уравнения. В окне Workfile можно дважды щелкнуть на переменной Resid (рис. 45). Далее, выбрать: VIEW/LINE GRAPH/, или, открыв окно с параметрами уравнения регрессии, выбрать: VIEW /ACTUAL,FITTED…/ACTUAL, FITTED…TABLE/ (рис. 46). Результат представлен на рис. 47. Другой вариант вывода (фактические, предсказанные значения переменных, остатки, график остатков) – рис. 48.

Рис. 45.

Рис. 46.

Рис. 47.

Рис. 48.

12. Для нахождения границ доверительного интервала в командной строке необходимо указать (рис. 49):

GENR XK = 5 * 1.05

GENR YFK = 4.53 +2.77*XK

GENR h = ((1 + 0.25^2)/1.6957^2) ^0.5

GENR CI = 2.31*(1.07/10^0.5)*h

В результате искомые границы определяются следующим образом:

YFKCI , т.е. от YFK+CI до YFK-CI (см. рис. 50).

Рис. 49.

Рис. 50.

13. Оформить отчет по занятию.

Отчет должен содержать: подробные пояснения расчетов, ссылки на используемые формулы, результаты работы Eviews в виде экранных копий, другую, необходимую на Ваш взгляд, информацию.

Практическое занятие № 3.

«Применение Eviews при построении и анализе линейной однофакторной модели регрессии»

Выполняется самостоятельно.

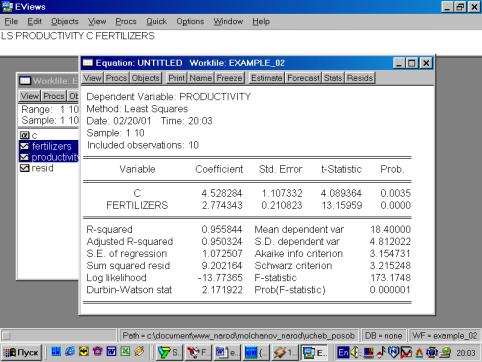
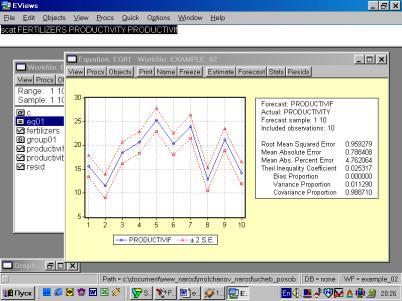
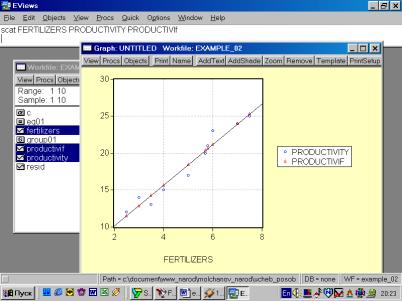
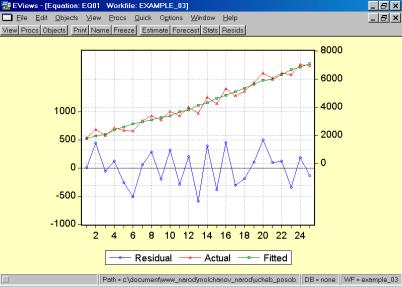
Результаты расчетов:

Рис. 51.

Рис. 52.

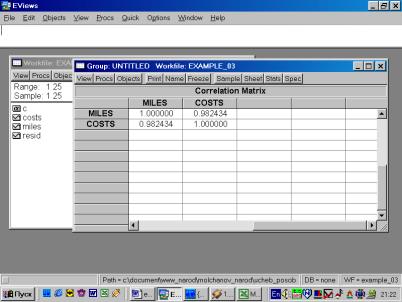
Рис. 53.

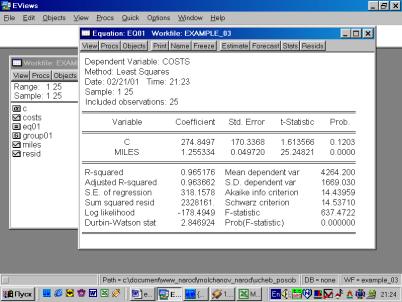
Рис. 54.

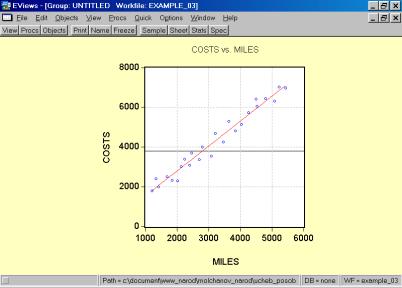
Рис. 55.

Рис. 56.

Рис. 57.

Практическое занятие № 4.

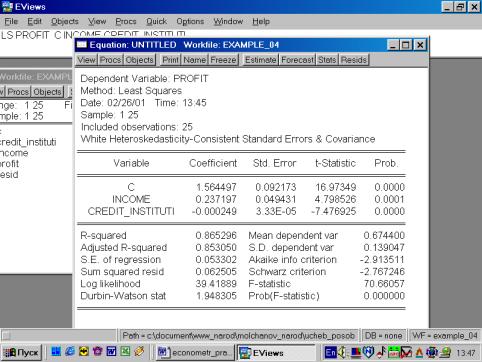
«Применение Eviews при построении и анализе многофакторной модели регрессии. Выявление мультиколлинеарности и гетероскедастичности в модели. Проверка спецификации модели»

Введем следующие обозначения:

    – прибыль кредитных организаций, %;

  - чистый доход на 1$ депозита;

– число кредитных учреждений.

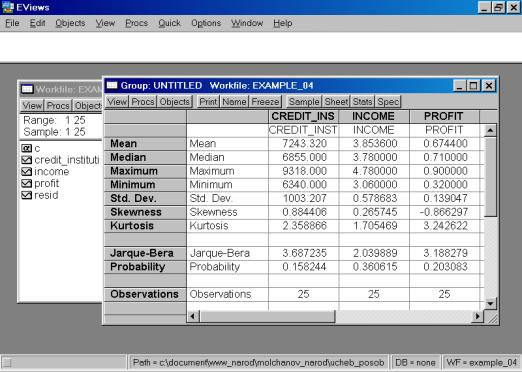
Рис. 58.

5.     Построить корреляционную матрицу для всех переменных, включенных в модель (рис. 59).

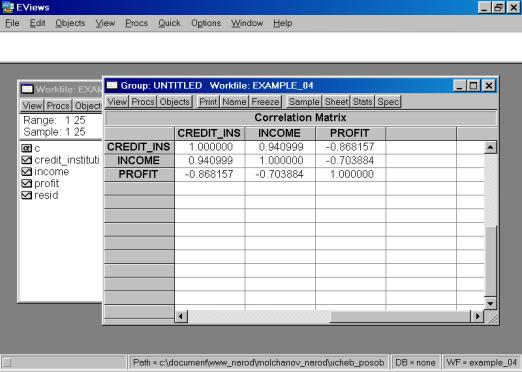
Рис. 59.

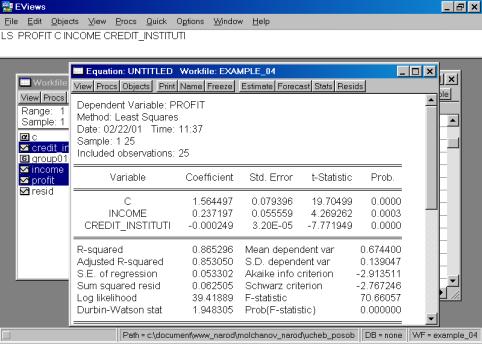
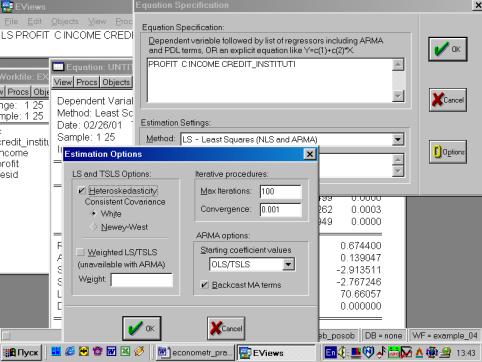
6.     Построить регрессионное уравнение МНК, в котором зависимая переменная – прибыль кредитных организаций, а независимые – чистый доход на 1$ депозита и число кредитных учреждений (рис. 60, 61).

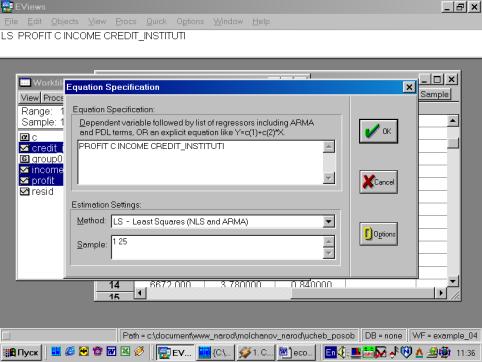
Рис. 60.

Рис. 61.

Уравнение примет следующий вид:

.

Подставим полученные оценки из итоговой формы вывода:

.

7.     Оценить статистическую значимость параметров полученного уравнения и всей модели в целом.

8.     Проверить наличие мультиколлинеарности в модели. Сделать вывод.

Мультиколлинеарность – это коррелированность двух или нескольких объясняющих переменных  в уравнении регрессии. 

Для проверки появления мультиколлинеарности  применяются два метода, доступные во всех статистических пакета.

Ø     Вычисление матрицы коэффициентов корреляции для всех объясняющих переменных. Если коэффициенты корреляции между отдельными объясняющими переменными  очень велики, то, следовательно, они коллинеарны. Однако, при этом не существует единого правила, в соответствии с которым есть некоторое пороговое значение коэффициента корреляции, после которого высокая корреляция может вызвать отрицательный эффект и повлиять на качество регрессии.

Ø     Для измерения эффекта мультиколлинеарности используется показатель VIF – «фактор инфляции вариации»:

ü 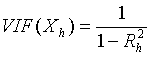        , где    - значение коэффициента множественной корреляции, полученное для регрессора  как зависимой переменной и остальных переменных . При этом степень мультиколлинеарности, представляемая в регрессии переменной , когда переменные  включены в регрессию, есть функция множественной корреляции между  и другими переменными .

ü     Если , то объясняющие переменные, коррелирующие между собой,  считаются мультиколлинеарными.

Существует еще ряд способов, позволяющих обнаружить эффект мультиколлинеарности:

Ø     Стандартная ошибка регрессионных коэффициентов близка к нулю.

Ø     Мощность коэффициента регрессии отличается от ожидаемого значения.

Ø     Знаки коэффициентов регрессии противоположны ожидаемым.

Ø     Добавление или удаление наблюдений из модели сильно изменяют значения оценок.

Ø     Значение F-критерия существенно, а t-критерия – нет.

Для устранения мультиколлинеарности может быть принято несколько мер:

Ø     Увеличивают объем выборки по принципу, что больше дан­ных означает меньшие дисперсии оценок МНК. Проблема реализации этого варианта решения состоит в трудности на­хождения дополнительных данных.

Ø     Исключают те переменные, которые высококоррелированны с остальными. Проблема здесь заключается в том, что воз­можно переменные были включены на теоретической основе, и будет неправомочным их исключение только лишь для то­го, чтобы сделать статистические результаты «лучше».

Ø     Объединяют данные кросс-секций и временных рядов. При этом методе берут коэффициент из, скажем, кросс-секционной регрессии и заменяют его на коэффициент из эквивалентных данных временного ряда.

Проделанные манипуляции позволяют предположить, что мультиколлинеарность может присутствовать (оценки  любой регрессии будут страдать от нее в определенной степени, если только все независимые переменные не окажутся абсолютно некоррелированными), однако в данном примере это не влияет на результаты оценки регрессии. Следовательно, выделять «лишние» переменные не стоит, так как это отражается на содержательном смысле модели.

9.     Проверить спецификацию модели. Объяснить полученные результаты.

Подробно теоретические вопросы, связанные с проблемами спецификации эконометрических моделей, были рассмотрены в лекционном курсе.

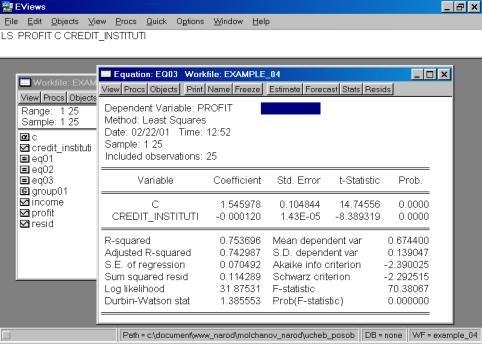
В нашем случае мы ограничимся тем, что попробуем исключить поочередно независимые переменные. Первой исключаем переменную CREDIT_INSTITUTI(рис. 62). Коэффициент при переменной INCOME изменил знак на противоположный.

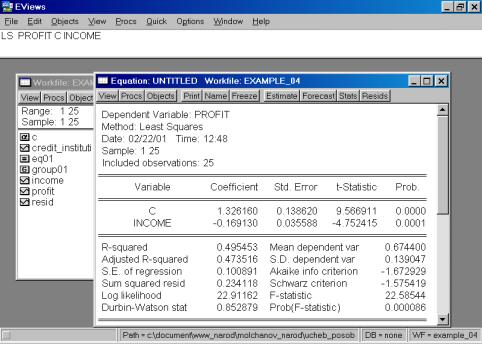
Рис. 62.

Рис. 63.

В случае исключения из первоначальной модели переменной INCOME, знак регрессионного коэффициента при переменой CREDIT_INSTITUTI остался без изменения (рис. 63). Представляется разумным разделять эффект двух независимых переменных на зависимую переменную в модели с совместным их влиянием в регрессионном уравнении. Данный пример иллюстрирует важность использования множественной регрессии вместо парной в случае, когда изучаемое явление существенно детерминирует несколько независимых переменных.

10. Проверить наличие гетероскедастичности в модели. Объяснить полученные результаты.

Проверкой на гетероскедастичность служит тест Голдфелда-Кванта. Он требует, чтобы остатки были разделены на две груп­пы из  наблюдений, одна группа с низкими, а другая – с высо­кими значениями. Обычно срединная одна шестая часть наблю­дений удаляется после ранжирования в возрастающем порядке, чтобы улучшить разграничение между двумя группами. Отсюда число остатков в каждой группе составляет , где  пред­ставляет одну шестую часть наблюдений.

Критерий Голдфелда-Кванта – это отношение суммы квадра­тов отклонений (СКО) высоких остатков к СКО низких остатков:

.

Этот критерий имеет распределение с  степе­нями свободы.

Следовательно, дисперсия коэффициентов запишется:

.

Отсюда если , мы трансформируем регрессионную мо­дель к виду:

.

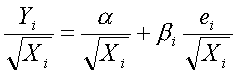Если , т.е. дисперсия увеличивается в пропорции к квадрату рассматриваемой переменной , трансформация при­обретает вид:

.

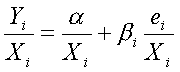Используя Eviews, можно провести проверку и устранение гетероскедастичности следующим образом:

Ø     Запустить стандартную регрессию.

Ø     Вычислить остатки.

Ø     Запустить регрессию с использованием квадрата остатков как зависимой переменной и оценить зависимую переменную  как независимую переменную (тестWhite).

Ø     Оценить nR², где n – объем выборки, R² – коэффициент детерминации.

Ø     Использовать статистику с одной степенью свободы (в EVIEWS – используется F – статистика) для проверки существенности отличия  nR² от нуля.

Ø     Основным способом устранения гетероскедастичности является применение взвешенного метода наименьших квадратов.

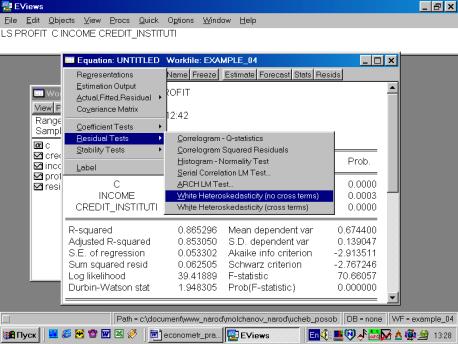
Выбираем тест White (см. рис. 64).

Рис. 64.

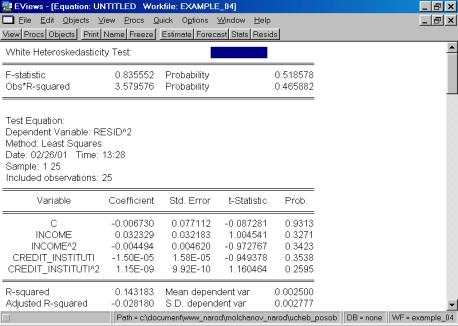
Итог формы вывода представлен на рис. 65.

Рис. 65.

Как следует из приведенной распечатки, вероятность ошибки первого рода равна 51,86%. Следовательно, нулевую гипотезу (об отсутствии гетероскедастичности) нельзя отклонить.

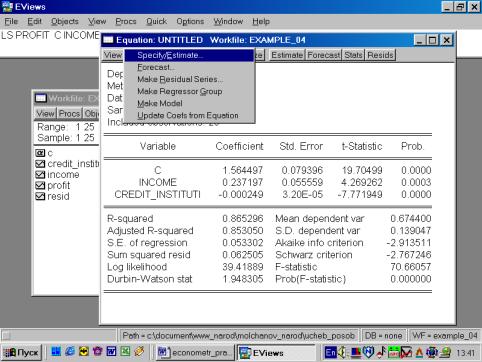
Рис. 66.

Рис. 67.

Появилось новое, переоцененное уравнение (рис. 68). Полученное уравнение можно вновь проверить по тесту White.

Рис. 68.

Практическое занятие № 5.

«Фиктивные переменные»

Иногда необходимо включение в регрессионную модель одной или более качественных переменных (например, разделение по полу: мужской и женский; по уровню образования: общее и профессиональное и т.д.).

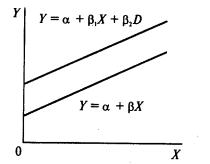
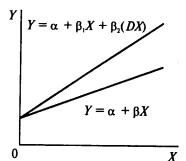
Фиктивные переменные бывают двух типов - сдвига и на­клона. Фиктивная переменная сдвига - это переменная, которая меняет точку пересечения линии регрессии с осью ординат в случае применения качественной переменной (рис. 69). Фиктивная пере­менная наклона - это та переменная, которая изменяет наклон линии регрессии в случае использования качественной перемен­ной (рис. 70). Оба типа фиктивных переменных будут иметь значение  или , когда наблюдения данных совпадают с уместной ко­личественной переменной, но будут иметь нулевое значение при совпадении с наблюдениями, где эта качественная переменная отсутствует.

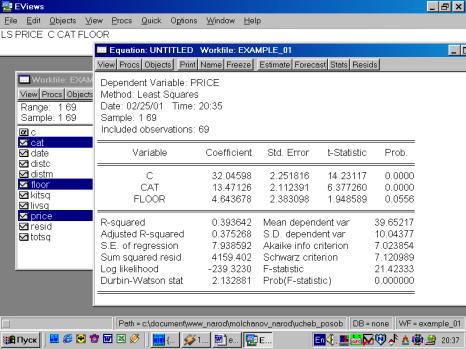
Пример 5. По данным примера  1 (файл example_01.xls.) дать интерпретацию бинарным, «фиктивным» переменным, принимающим значения 0 или 1: floor – принимает значение 0, если квартира расположена на первом или последнем этаже,  cat –принимает значение 1, если квартира находится в кирпичном доме.

.

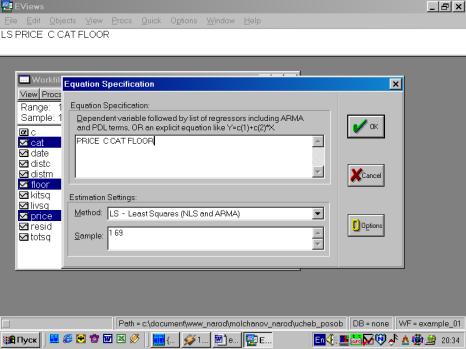
Рис. 71.

Рис. 72.

Используя результаты оценивания уравнения, содержащиеся в форме вывода (рис. 72), можно записать такое уравнение:

.

Как же можно интерпретировать полученные результаты? Полученный коэффициент при CAT означает, что квартиры в кирпичных домах стоят в среднем на $13471 дороже аналогичных квартир в панельных домах. Коэффициент при FLOOR может быть интерпретирован так: квартиры на не первом/последнем этажах стоят в среднем на $4644 дороже аналогичных, расположенных на первом/последнем этажах.