| Главная » Статьи » Прочие |
Приемы моделирования Прежде чем приступать к моделированию, освойте предназначенные для этого инструменты. В следующих разделах дается краткий обзор основных средств, которые включены практически во все графические приложения. Многие пакеты поддерживают и другие возможности; некоторые оснащены лишь частью из того, что описывается в книге. Однако знакомство с базовым набором позволит вам быстро освоить любое программное обеспечение. Очень часто при описании инструментов моделирования возникает путаница, связанная с терминологией. Один и тот же инструмент в разных пакетах может называться по-разному. В таких случаях я привожу список соответствующих терминов из наиболее распространенных систем. Основные элементы полигональных моделей Метод полигонального моделирования, используемый во многих пакетах, позволяет создавать великолепные персонажи. Благодаря ему вы избавитесь от проблем, связанных с топологией модели, чего не обеспечивают многие программы, работающие с патчами. Суть полигонального моделирования очень проста. Модели подобного типа состоят из трех основных элементов (примитивов): вершин, ребер и многоугольников. Для манипулирования данными элементами разработано несколько методов, которые подробно рассматриваются ниже. Вершины Вершина - это одномерный объект, точка, расположенная в пространстве (рис. 2.5). Если соединить две вершины, получится ребро (рис. 2.6). Некоторые программы моделирования предлагают дополнительные операции над вершинами, например Extrude (Экструдирование) и Bevel(Формирование скоса), показанные на рис. 2.7 и 2.8 соответственно; в обоих случаях создаются дополнительные ребра и многоугольники. Ребра Ребро определяется двумя вершинами. Когда объект изображается в виде проволочного каркаса, все его ребра видны. В сущности, они представляют собой линии и являются двумерными объектами. Три ребра или более образуют многоугольник. Над ребрами можно выполнять ряд операций. В их число входят уже названные Extrude и Bevel, операция Collapse (Стягивание), которая удаляет ребро, превращая его в вершину. Кроме того, для ребер предусмотрена операция Cut/Connect (Разрезание/Соединение): существующие ребра разрезаются пополам, а точки разреза соединяются новым ребром. Результаты выполнения этих операций показаны на рис. 2.9-2.12. Многоугольники Многоугольник определяется тремя или более ребрами (рис. 2.13). По сути он является плоским трехмерным объектом. Для выполнения рендеринга поверхность должна состоять из многоугольников. Большинство пакетов разрешает работать с многоугольниками, имеющими более трех ребер, однако обычно в процессе визуализации такие примитивы все равно разбивается на треугольники. Над многоугольниками можно выполнять следующие операции. Проиллюстрированные рис. 2.14-2.16 операции Extrude (Экструдирование), Inset (Вставка) и Bevel (Формирование скоса) являются вариантами одной и той же операции - создания дополнительного многоугольника на основе того или иного элемента исходного. Отличие заключается в том, что происходит с исходным многоугольником. При экструдировании часть его выдвигается наружу или перемещается внутрь обычно вдоль нормали к поверхности (то есть вдоль перпендикуляра к грани). Когда выполняется вставка, масштаб исходного многоугольника, как правило, уменьшается, и полученная фигура располагается в плоскости исходной. Операция формирования скоса по сути является комбинацией первых двух, поскольку исходный элемент масштабируется и перемещается. В результате появляются новые грани. Кроме того, к многоугольникам применяется операция Collapse (Стягивание), которая удаляет многоугольник, стягивая его в одну вершину (рис. 2.17).
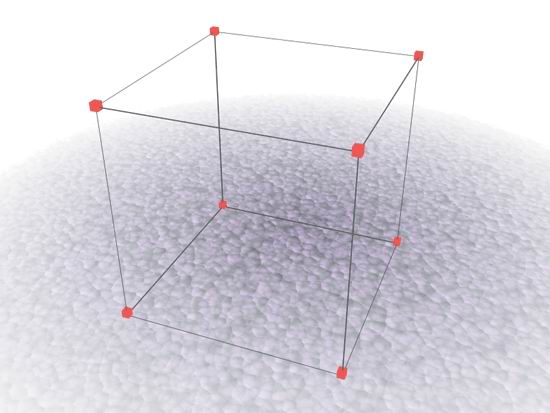
Рис. 2.5. Вершины
Рис. 2.6. Ребра
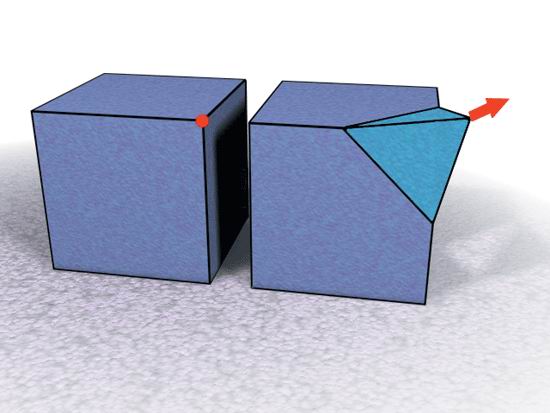
Рис. 2.7. Операция Extrude над вершиной
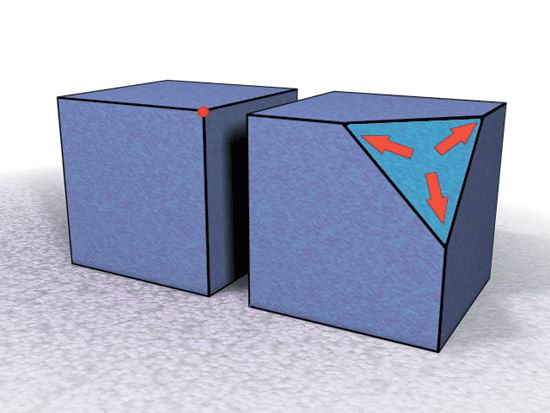
Рис. 2.8. Операция Bevel для скоса вершины
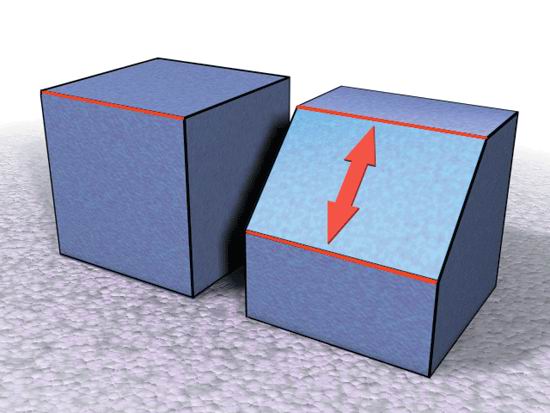
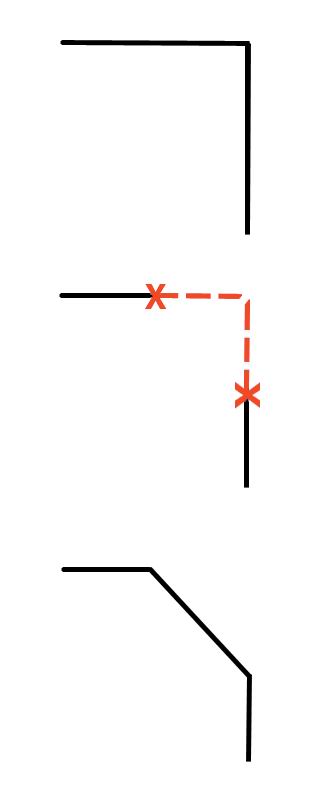
Рис. 2.9. Операция Extrude над ребром
Рис. 2.10. Операция Bevel для скоса ребра
Рис. 2.11. Операция Collapse над ребром
Рис. 2.12. Операция Cut/Connect над ребром
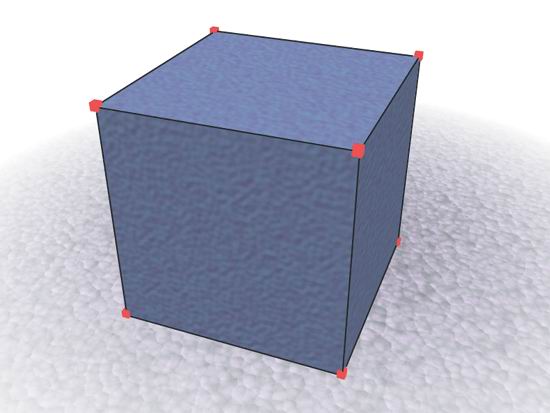
Рис. 2.13. Многоугольники куба
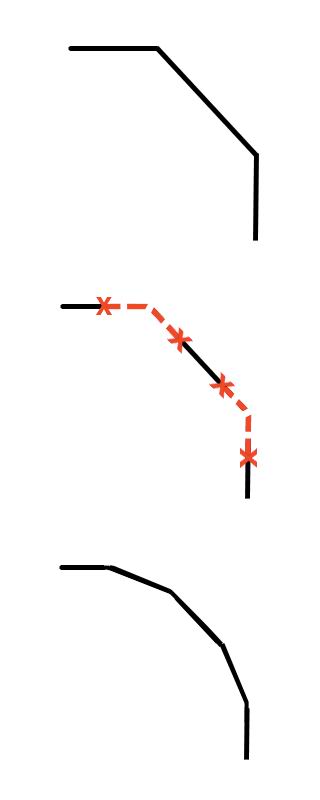
Рис. 2.14. Операция Extrude над многоугольником
Рис. 2.15. Операция Inset над многоугольником
Рис. 2.16. Операция Bevel над многоугольником
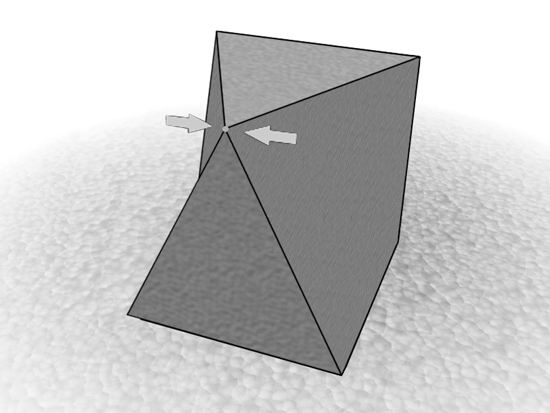
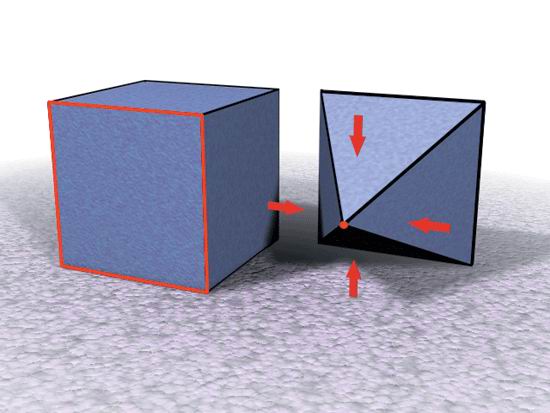
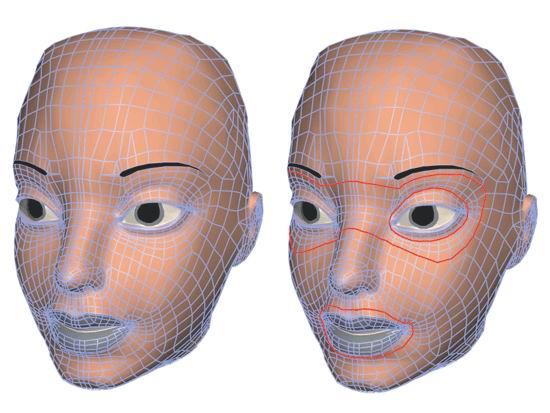
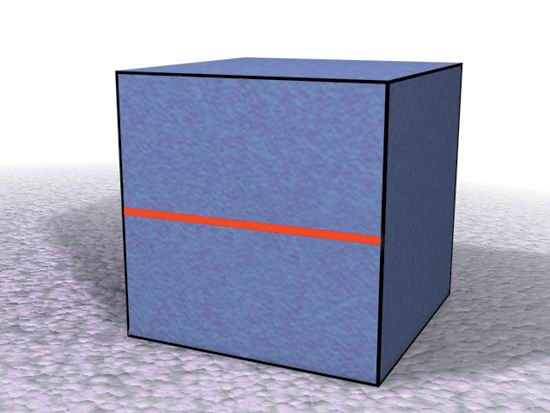
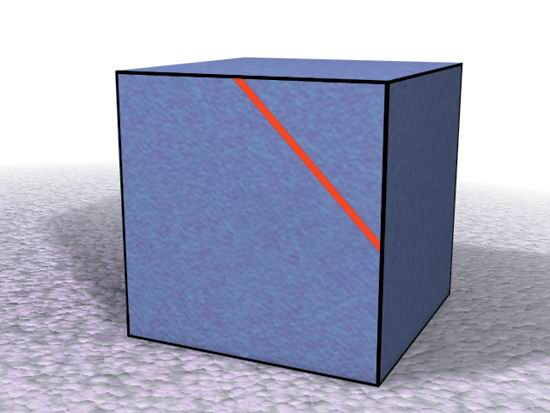
Рис. 2.17. Операция Collapse над многоугольником Методы полигонального моделирования Теперь, когда вы ознакомились с основными операциями, процесс моделирования на основе многоугольников уже не вызовет особых затруднений. Обычно создается какой-либо базовый объект, например параллелепипед, цилиндр или сфера. Затем он модифицируется при помощи ряда операций и приобретает более сложную форму, соответствующую очертаниям персонажа. От простого к сложному При конструировании полигональных поверхностей рекомендуется начинать с небольшого количества элементов и потом добавлять их по мере необходимости. Многие разработчики начинают с примитивов: параллелепипеда или сферы, - а затем придают поверхности желаемую форму, вводя новые детали. Занимаясь моделированием, повторяйте, как молитву, следующую фразу: «Моя цель - достичь максимального результата, используя минимальное количество элементов». Создатели персонажей для интерактивных игр оказываются в наиболее трудном положении, поскольку их модели должны быть как можно более простыми. Если вы хотите узнать, как создаются несложные, но качественные модели, посидите нескольких часов рядом с разработчиком графики для компьютерных игр. Замкнутые контуры, образуемые ребрами Изучая методы конструирования полигональных моделей, особое внимание обратите на замкнутые контуры, составленные из ребер (рис. 2.18). Они ограничивают некоторую область поверхности. Например, при конструировании лица замкнутый контур используется для очерчивания рта, бровей и глазных впадин (рис. 2.19). При моделировании тела эти контуры определяют форму туловища, рук и ног. Чтобы понять, что такое замкнутый контур, вспомните, как на топографической карте изображается рельеф. Уровень возвышенности имеет вид замкнутой кривой. Если такую карту перенести в программу трехмерного моделирования и заменить кривые уровней на замкнутые контуры, составленные из ребер, неровности приобретут объем. Обычно замкнутые контуры создаются путем разрезания пополам двух ребер и соединения точек разреза новым ребром. Эта операция оказывает существенное влияние на поведение модели в дальнейшем. При разрезании противоположных сторон прямоугольника получается два многоугольника с четырьмя ребрами (четырехугольника), см. рис. 2.20. Когда соединяют два смежных ребра, образуются треугольник и пятиугольник, которые могут стать источником неприятностей при деформировании персонажа (рис. 2.21). Лучше всегда создавать четырехугольники, поскольку
Рис. 2.18. Замкнутые контуры
Рис. 2.19. Очертания рта и глазных впадин, сформированные с помощью концентрических линий
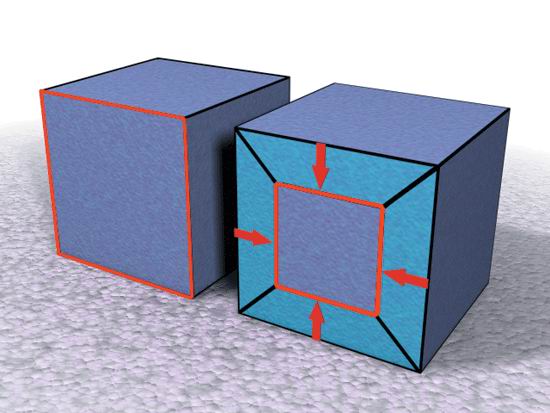
Рис. 2.20. Результат разрезания и последующее соединение противоположных сторон прямоугольника
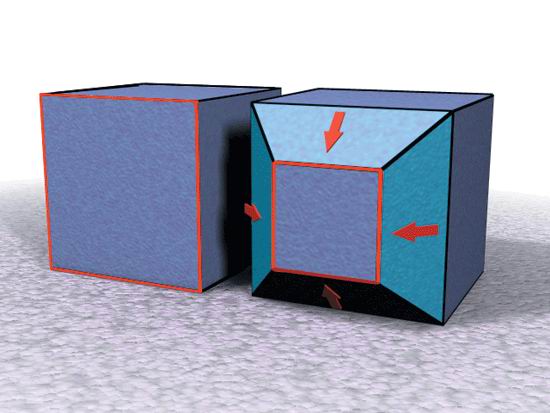
Рис. 2.21. Треугольник и пятиугольник, образованные при соединении прилегающих сторон. их деформации более предсказуемы, чем изменения поверхностей, составленных из треугольников. При построении замкнутых контуров старайтесь обойтись без соединения смежных ребер, иначе при анимации могут возникнуть нежелательные искажения. Операция Subdivide для поверхностей Большинство разработчиков персонажей для кино- или видеофильмов стремятся к тому, чтобы их модели имели сглаженную поверхность и выглядели как можно более естественно. На первый взгляд кажется, что этого трудно добиться, поскольку дополнительные элементы усложняют манипулирование поверхностью. К счастью, имеются специальные инструменты, которые позволяют почти автоматически преобразовать модель с низким разрешением в модель с высоким разрешением, если исходный образец имеет упорядоченную конструкцию. Этот метод разделения многоугольников (или уплотнения каркаса) называется в различных системах трехмерного моделирования по-разному.
Превращение многоугольников в патчи В процессе дробления полигональной поверхности программа создает новые элементы, которые необходимо правильно разместить. Формирование дополнительных многоугольников регулируется рядом правил. В теории все выглядит просто: три или четыре точки, не лежащие на одной прямой, интерполируются кривой более высокого порядка, чем прямая, и в результате получается такая же аппроксимация поверхности, как и при использовании патчей. Простейший способ вычислить местоположение дополнительных элементов - отсечь определенные углы (рис, 2.22-2.23). Резчик по дереву
Рис. 2.22. Операция разделения двух линий
Рис. 2.23. Многократно сглаженные прямые обычно начинает со стесывания углов деревянного чурбана. Если вы научитесь при помощи математических формул скруглять резкие выступы на модели виртуального героя, ее поверхность станет более гладкой. Метод, позволяющий это сделать, называется отсечением углов. Берутся серединные точки или центры многоугольников, образующих поверхность объекта, и соединяются путем создания промежуточных многоугольников: одна фигура превращается в четыре, четыре - в шестнадцать и т.д. На каждом шаге происходит отсечение углов, в результате чего объект становится более гладким (рис. 2.24-2.25). Одно из любопытных свойств данной операции состоит в том, что если выполнять ее бесконечно долго, получится такая же поверхность, как при использовании пат-чей на основе В-сплайнов. Вдумайтесь в смысл предыдущего предложения. С математической точки зрения, сглаженная полигональная поверхность - то же самое, что утверждать, что лучше использовать патчи, а не многоугольники, напомните ему об этом пикантном факте. Естественно, бесконечное количество операций не может проделать даже самый мощный компьютер, так что ограничьтесь двумя или тремя проходами. Обычно этого достаточно, чтобы поверхность выглядела на кино- или телеэкране абсолютно гладкой.
Рис. 2.24. Разделение граней
Рис. 2.25. Сочетание треугольников и четырехугольников, полученное благодаря сглаживанию Сглаживание поверхности и анимация Единственная проблема, возникающая в результате дробления полигональной поверхности, заключается в том, что дополнительные детали «утяжеляют» модель персонажа. Имитация быстрых движений и проведение деформаций становятся практически неосуществимыми. Для решения этой проблемы придумано несколько приемов. Большинство из них основано на том, что поверхность персонажа сглаживается после создания анимации, но до визуализации. Некоторые объектно-ориентированные пакеты, такие как 3D Studio MAX, LightWave и Houdini, позволяют сглаживать поверхность в любой момент, но обычно дизайнеры делают это после деформирования модели и создания анимации. Многие пакеты дают возможность управлять модификатором сглаживания. Если модификатор выключен, модель персонажа имеет низкое разрешение, и анимация проводятся быстро. При включенном модификаторе разрешение модели становится более высоким, и ее можно визуализировать. Поскольку каркас уплотняется уже после деформации модели, растяжений и складок при сглаживании не возникает. Такой способ анимации (его называют методом разделения поверхностей) проиллюстрирован рис. 2.26: чтобы анимация проходила в правильном темпе, используются модели с низким разрешением (слева). Для получения модели, имеющей реалистичный вид, после деформирования и перед визуализацией производится сглаживание (справа).
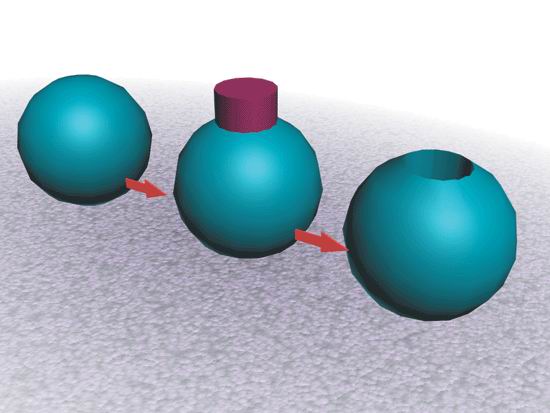
Рис. 2.26. Анимация методом разделения поверхностей Другие пакеты, например Nichimen и Light Wave, позволяют автоматически сглаживать поверхность уже во время визуализации (как описано в предыдущем примере). Еще один способ решения данной проблемы - одновременно работать с двумя моделями, имеющими низкое и высокое разрешение. Первая из них подвергается анимации. Затем кривые анимации переносятся на вторую модель, и выполняется визуализация. Единственная проблема заключается в том, что деформации модели с низким разрешением немного отличаются от деформаций сглаженной модели, и в результате могут возникнуть растяжения и другие мелкие неприятности. Ужасные булевские операции Да, это истинная правда, булевские операции - настоящий кошмар. Они есть во многих пакетах полигонального моделирования, что позволяет достаточно легко складывать и вычитать тела (рис. 2.27). Может быть, это и удобно при работе с объектами неизменной формы, но не в том случае, когда объекты приходится деформировать. После применения к модели булевской операции возникает масса ненужных многоугольников. Если вы посмотрите на след, появившийся в результате ее проведения, то увидите огромное количество крошечных граней, корректирующих изъяны на стыках объектов. Эти многоугольники практически не влияют на вид модели, но делают ее вдвое, а то и втрое «тяжелее». К тому же, при сглаживании булевские поверхности покрываются складками из-за нежелательных добавочных элементов, что показано на рис. 2.28. Сравните с этим изображением рис. 2.29, где проиллюстрирован результат выполнения аналогичных действий, но без использования булевских операций. Как видите, поверхность вокруг отверстия хорошо сглажена.
Рис. 2.27. Вычитание цилиндра из сферы с помощью булевской операции Даже если булевские операции применяются к моделям с низким разрешением, на швах получается сущее безобразие. После сглаживания поверхность, к которой применяли операции этого типа, выглядит как шрам, оставленный плохим хирургом. Возможно, такой рубец будет уместен при моделировании Франкенштейна, но если у вас другие планы, избегайте булевских операций. Вместо них находчивые разработчики используют стандартные инструменты полигонального моделирования. При создании выступа примените операцию формирования скоса или экструдируйте многоугольники наружу. Если в объекте необходимо вырезать отверстие, экструдируйте многоугольники внутрь или сформируйте внутренний скос. Это позволит избежать проблем при сглаживании.
Рис. 2.28. Результат сглаживания булевских поверхностей
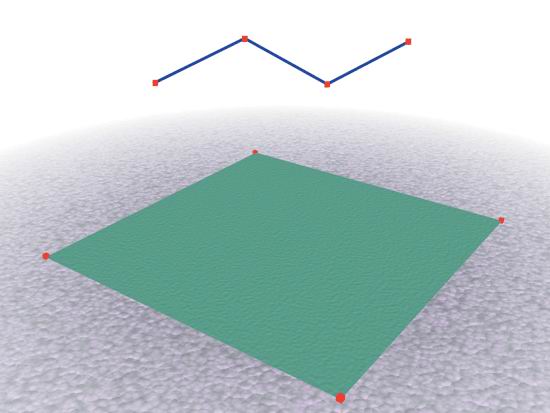
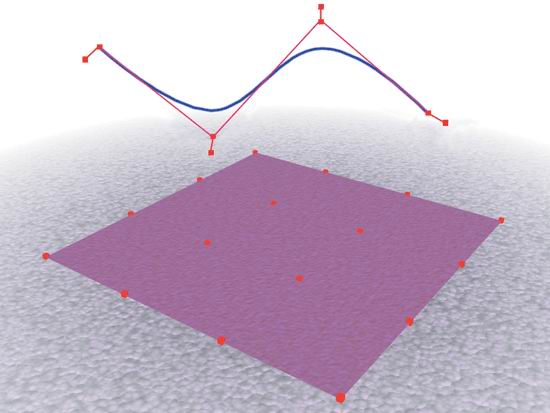
Рис. 2.29. Получение хорошо сглаженной поверхности Моделирование при помощи патчей Моделирование при помощи патчей - еще один великолепный способ создания персонажей. Патчи -это фрагменты поверхности, определяемые кривыми. Кривые могут быть линейными, фундаментальными, В-сплайнами или Безье-кривыми. Обычно патчи имеют вид четырехугольника или совокупности четырехугольников. Как уже говорилось, кривые и поверхности определяются их порядком, от которого зависит возможность управления ими. Линейные кривые (рис. 2.30). Это кривые первого порядка, состоящие из последовательности отрезков, соединяющих управляющие вершины. Кривые, определяющие поверхность, эквивалентны ребрам полигонального каркаса. Приемы моделирования Фундаментальные кривые (рис. 2.31). Это кривые второго порядка, проходящие через управляющие вершины, в каждой из которых задана касательная. Пат-чи, созданные на основе таких кривых, имеют четыре ряда вершин по каждому направлению, итого 16 точек. Управляющие вершины выходят за границы патча. Это необходимо из-за погрешностей интерполяции в конечных точках; дополнительные вершины определяют форму кривой.
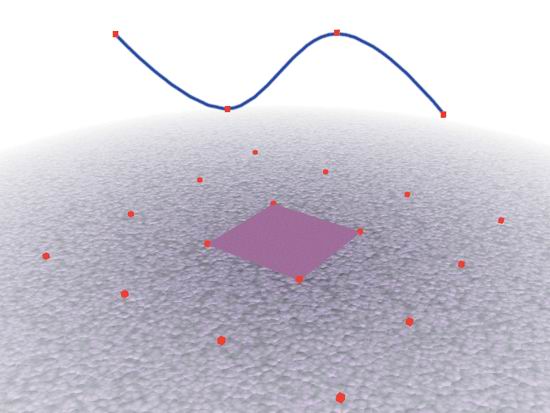
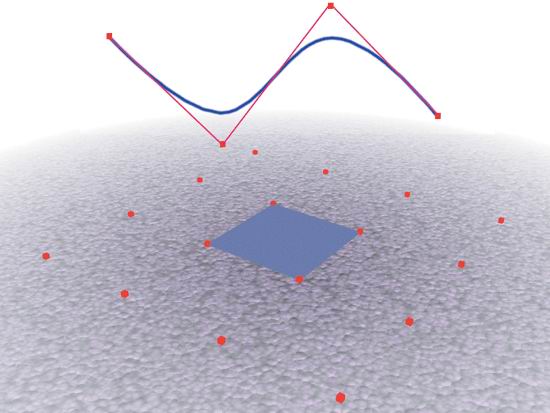
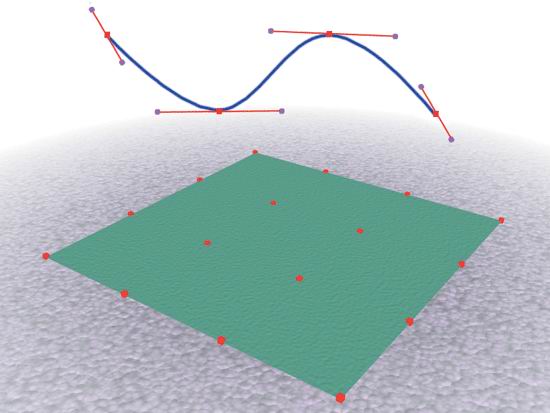
Рис. 2.30. Линейная кривая В-сплайны (рис. 2.32). Кривые третьего порядка, которые редко проходят через управляющие вершины. Из-за того, что управляющие вершины находятся на некотором расстоянии от кривой, манипулирование поверхностью может быть затруднено. В кривых данного типа вершины называютсяузлами. Как и в случае с фундаментальными кривыми, интерполяция выполняется не далее конечных точек, то есть для определения кривизны поверхности патча требуются дополнительные вершины, расположенные за его границами. Кривые Безье (рис. 2.33). Это тоже кривые третьего порядка, аналогичные используемым в популярных программах рисования типа Adobe Illustrator. Кривая проходит через каждую управляющую вершину, в которой задана касательная; имеются два манипулятора, позволяющие управлять формой кривой по обе стороны от вершины. С их помощью можно выполнить интерполяцию в конечных точках, поэтому вершины располагаются на краях патча.
Рис. 2.31. Фундаментальная кривая
Рис. 2.32. В-сплайн Одно из преимуществ кривых Безье состоит в том, что манипуляторы позволяют более гибко управлять кривизной и формировать весь спектр поверхностей - от гладких до покрытых глубокими складками. Другим достоинством является ограниченность области действия манипуляторов: изменения на одном фрагменте модели не влияют на остальную ее часть. Кроме того, при моделировании широко используются NURBS-кривые (рис. 2.34).
Рис. 2.33. Кривая Безье
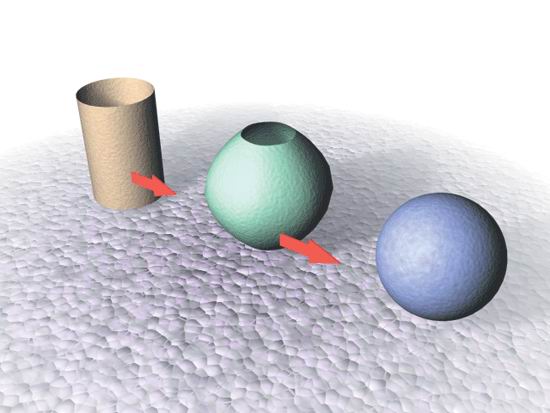
Рис. 2.34. Неоднородная форма В-сплайна Регулярные поверхности Проще всего при помощи патчей создавать регулярные поверхности -гладкие и состоящие, как правило, из единственного патча. Однопатчевые модели конструируют путем модификации примитивов; например, из сферы делают голову, а из цилиндра - тело персонажа. Регулярные поверхности особенно хороши тем, что предельно упрощают наложение текстуры. Осям U и V поверхности можно сопоставить непосредственно координатные оси X и Y изображения. Если объект создан только из одной регулярной поверхности, можно не применять проекционные координаты отображения к поверхности, как это делается для нерегулярного полигонального каркаса. В процессе патч-моделирования относитесь к регулярным поверхностям как к огромным кускам упаковочной бумаги. Все, что можно обернуть одним листом, представимо в виде регулярной поверхности. Например, для создания цилиндра достаточно свернуть лист в рулон. Создавая сферу, необходимо сжать края свернутого листа (рис, 2.35-2.36).
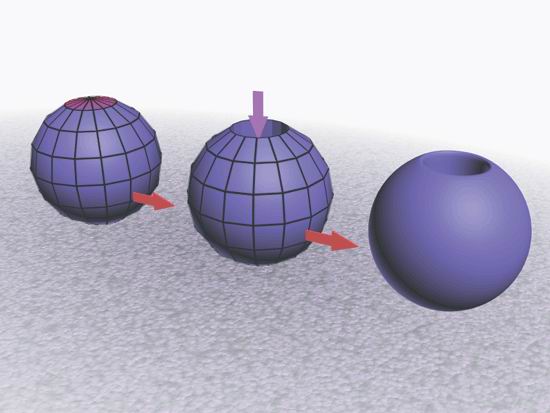
Рис. 2.35. Цилиндрическая поверхность, полученная из патча
Рис. 2.36. Формирование сферы путем стягивания поверхности к крайним вершинам Источник: http://www.lessonsflash.ru/animation/1-2.htm#15 | |
| Просмотров: 1291 | | |
| Всего комментариев: 0 | |